The Incredible Two Pointers Technique

Hey there, fellow learners! I’m Artem, and today’s lesson is all about the incredible Two Pointers technique.

What is the Benefit of the Two Pointers Technique?

Before we dive deep into the details, let’s first talk about the benefit of the Two Pointers technique. This technique can dramatically improve the performance of your solutions, allowing you to optimize algorithms with time complexities like O(n^2) or O(n log n) down to O(n) in many cases.

What is the Two Pointers Technique?

To understand the Two Pointers technique, you should have a basic grasp of data structures such as arrays and linked lists and be comfortable with Big O notation. If you’re not sure about Big O, I recommend watching my video on the topic for a refresher.

The Two Pointers technique uses two variables (or “pointers”) that point to different positions in an array or list. These pointers move through the collection based on certain conditions, allowing you to keep track of multiple elements simultaneously.

How It Works

In Figure 1, you can see how arrays look under the hood. Each element has its index, value, and memory address.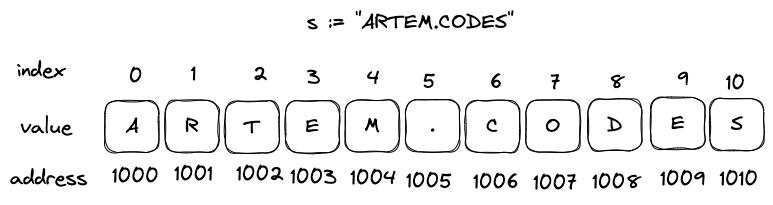

In Figure 2, we have two pointers, left and right, pointing to addresses 1000 and 1004, respectively. This means that if the element at address 1000 is updated, the left pointer will reflect this change. The same applies to the right pointer.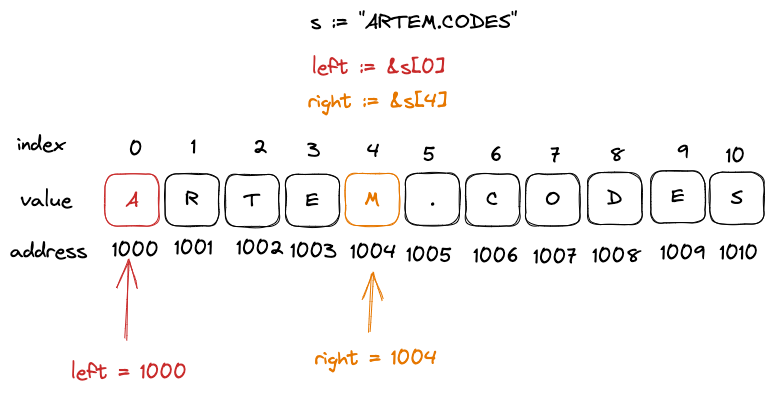

These pointers allow you to track two elements simultaneously as you iterate through a collection. This technique is most commonly used with arrays and linked lists but isn’t generally applicable to non-linear data structures.

In many cases, these pointers are called left and right or slow and fast. Wondering why? Keep reading!

Example Showing the Performance Difference

Let’s consider a problem like Leetcode’s Two Sum II.

Solution #1: Brute Force - Space: O(1), Time: O(n^2)

In this approach, we check all possible combinations of two elements in the array. This is quite inefficient because the time complexity is O(n^2). Let’s run a benchmark to see how long it takes.

// Brute-force approach
func twoSum(nums []int, target int) []int {
    n := len(nums)
    for i := 0; i < n-1; i++ {
        for j := i + 1; j < n; j++ {
            if nums[i]+nums[j] == target {
                return []int{i+1, j+1}
            }
        }
    }
    return []int{}
}

Benchmark results for the brute force solution:

goos: darwin
goarch: amd64
pkg: github.com/bukhavtsov/youtube/two-pointers/two_sum_quadratic
BenchmarkTwoSum10-8      	52684279	        23.03 ns/op
BenchmarkTwoSum100-8     	16249501	        71.73 ns/op
BenchmarkTwoSum1000-8    	 2671320	       441.8 ns/op
BenchmarkTwoSum10000-8   	  269739	      4381 ns/op
PASS

Solution #2: Two Pointers - Space: O(1), Time: O(n)

Now let’s solve the same problem using the Two Pointers technique. This approach takes advantage of the fact that the array is sorted, allowing us to reduce the time complexity to O(n).

// Two Pointers approach
func twoSum(numbers []int, target int) []int {
    left, right := 0, len(numbers)-1
    for left < right {
        sum := numbers[left] + numbers[right]
        if sum == target {
            return []int{left + 1, right + 1} // To match 1-indexing
        } else if sum < target {
            left++
        } else {
            right--
        }
    }
    return []int{-1, -1}
}

Benchmark results for the Two Pointers solution:

goos: darwin
goarch: amd64
pkg: github.com/bukhavtsov/youtube/two-pointers/two_sum_linear
BenchmarkTwoSum10-8      	56371071	        21.93 ns/op
BenchmarkTwoSum100-8     	52781440	        20.58 ns/op
BenchmarkTwoSum1000-8    	58837300	        20.83 ns/op
BenchmarkTwoSum10000-8   	55983619	        21.22 ns/op
PASS

Details of the Two Pointers Solution

The Two Pointers approach optimizes performance by eliminating unnecessary iterations. Here’s how it works:

• Start with two pointers: one (left) pointing to the smallest element, and another (right) pointing to the largest.
• On each iteration, check the sum of the elements at the pointers.
  • If the sum is greater than the target, move the right pointer to the left (to decrease the sum).
  • If the sum is smaller than the target, move the left pointer to the right (to increase the sum).

This process continues until the correct pair is found.

Problem: Finding the Middle Element with Fast & Slow Pointers

In this section, we’ll tackle a common problem using fast and slow pointers: finding the middle element of a linked list. This is a great example of how Two Pointers can be adapted for different scenarios.

Problem: Leetcode’s Middle of the Linked List

Fast & Slow Pointers Solution

In this approach, one pointer moves twice as fast as the other. By the time the fast pointer reaches the end, the slow pointer will be in the middle.

func middleNode(head *ListNode) *ListNode {
    fast := head
    slow := head
    for fast != nil && fast.Next != nil {
        fast = fast.Next.Next
        slow = slow.Next
    }
    return slow
}

Summary

The Two Pointers technique is a powerful optimization tool for solving problems efficiently. As shown by the benchmarks, this approach offers consistent performance with minimal time complexity compared to brute-force methods. Whether you’re finding pairs in a sorted array or locating the middle of a linked list, Two Pointers can help you solve problems faster and more elegantly.

Next steps? Try using this technique in your own algorithms and see how it can optimize your solutions!